Summary
This project optimises fuel blending for energy systems on a feed-forward network of inputs, intermediate storage, and outputs. This problem class, called a pooling problem, is an optimization challenge of blending petrochemical feeds to maximise profit while meeting environmental standards. In 1989, Texaco estimated that integrating mathematical optimization into fuel blending refinery operations led to a yearly savings of 30 × 10^6 $USD (Misener and Floudas, 2009); the continued monetary advantage to process industries are associated with high-throughput operations.
What is the challenge?
Industrially-relevant instantiations of the pooling problem are large-scale nonconvex MINLP with many bilinear terms. There is a relatively long time to explore the search space in the design phase of a petrochemical plant and high reward for fractional improvements to the best feasible solution; we address the problem using deterministic global optimization algorithms.
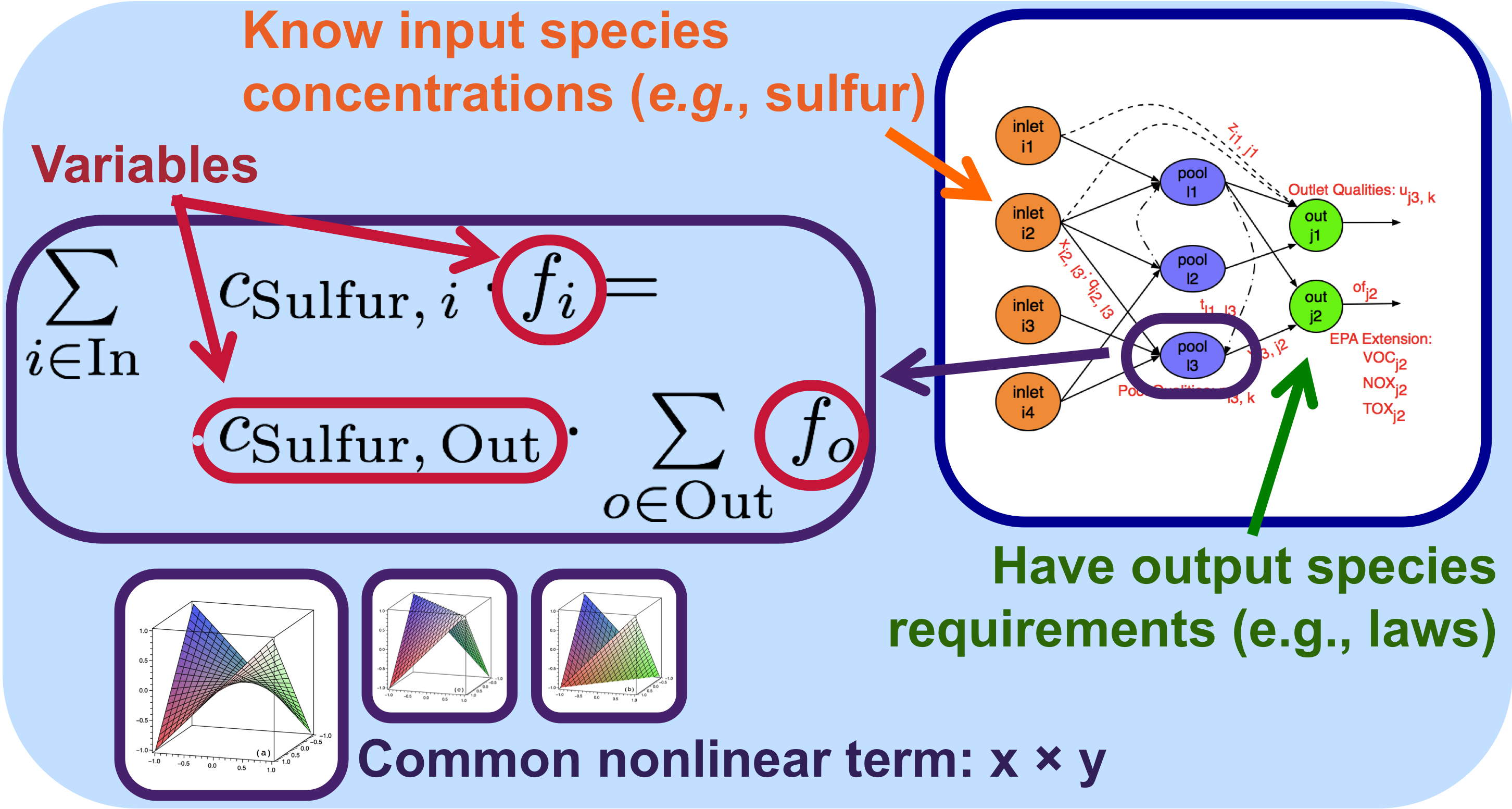
An example pooling problem network with inputs, intermediate storage, and outputs is illustrated in the upper right-hand corner of the figure above. The complexity of the pooling problem comes from the mass balances at the intermediate storage nodes (pools) where nonconvex bilinear terms arise from multiplying species concentrations with flow rates.
What contributions have we made?
We have globally optimized a variety of interesting and challenging pooling problems including those with applications to: the USA Environmental Protection Agency: Complex Emissions Model; mutable network topology; crude oil scheduling; hybrid energy systems. We addressed these large-scale instances using a piecewise-linear approach. Our original work was intuition-drived, but we recently rigorously proved that these problems are rooted in piecewise-defined functions (Baltean-Lugojan and Misener, 2017).
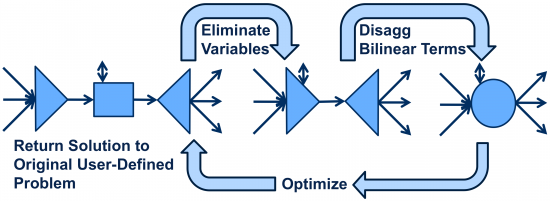
For more general classes, we have designed automatic reformulation steps to uncover special mathematical structure (Ceccon, Kouyialis, and Misener, 2016). While the transformations shown below (eliminating variables and disaggregating bilinear terms) may be implemented generically and applied universally, the reformulations are specifically targeted at enhancing algorithm performance on process networks problems. We have motivated the advantage of these transformations through examples of modular water networks design problems (Misener and Floudas, 2013) and demonstrated their relationship to the Reformulation Linearisation Technique with extensive computational study (Misener and Floudas, 2015).
We’ve also developed a plugin for the open-source optimization solver GALINI that solves industrially-relevant instances of the pooling problem (Ceccon and Misener, 2022).
Where do we go from here?
We have lots of challenging variations on the pooling problem which push the limits of currently-available algorithms; consider working with us! We continue our drive towards developing effective solution strategies for the pooling problem and its variants.
Collaborators
- Prof Christodoulos A Floudas (PhD advisor)
- Dr Radu Baltean-Lugojan, Dr Francesco Ceccon, Dr Georgia Kouyialis (piecewise-linear analysis and structure detection)
- Prof Chrysanthos Gounaris (USA Environmental Protection Agency Complex Emissions)
- Dr Jie Li (Crude Oil Scheduling)
- Dr Richard Baliban, Dr Josephine Elia (Hybrid Energy Systems)
- Dr Jeffrey Thompson (Webtool APOGEE)
Freely-Available Webtool
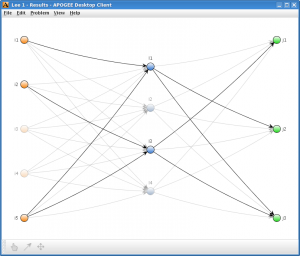APOGEE (GUI shown left), solves: generalised; extended; standard pooling problems. This class of global optimization problem is highly relevant to petrochemical applications including: crude oil scheduling; refinery operations; hybrid energy systems.
Dr Radu Baltean-Lugojan and Dr Francesco Ceccon have also made their code publicly available on the Computational Optimization Group Github account.
