Bayesian optimization with dimension scheduling: Application to biological systems

Student Lead: Doniyor Ulmasov (MSc, 2015)

This project is also highlighted here by the Sargent Centre for Process Systems Engineering.

Bayesian optimization

Bayesian Optimization (BO) is a data-efficient, global black-box optimization method optimising an expensive-to-evaluate fitness function; BO uses Gaussian Processes (GPs) to describe a posterior distribution over fitness functions from available experiments. An acquisition function is applied to the GP posterior distribution over fitness functions to suggest the next (optimal) experiment.

Testing biological hypotheses via parameter estimation

Dynamic models of biological processes allow us to test biological hypotheses while running fewer costly, real-world experiments. We consider estimating biological parameters, e.g., reaction rate kinetics, by minimizing the squared error between model and experimental data points. Specifically, we propose BO for efficient parameter estimation of a dynamic microalgae metabolism model (Baroukh et al., 2014). The forcing function is based on light exposure and nitrate input; experimental data has been collected for measurable outputs including lipids, carbohydrates, carbon organic biomass, nitrogen organic biomass and chlorophyll. But our method is general and may be applied to any process model.

There are several timescales for collecting microalgae metabolism data: an experiment may take 10 days while each model simulation of Baroukh et al. (2014) runs in a fraction of a second. BO is traditionally applied to functions with an expensive evaluation costs, e.g., running a 10 day experiment, but the objective of this paper is testing biological hypotheses; we are specifically interested in running the simulation model many times for parameter estimation.

Key Idea: Improve a small set of dimensions at each iteration

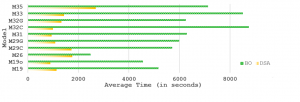
Average computation time of DSA and traditional BO for all models. DSA results in a substantial computational speed-up.

In biological parameter estimation, Bayesian Optimization (BO) is challenging because the parameters interact nonlinearly and the broad parameter bounds result in a huge search space. Due to the high problem dimensionality (in this context, 10 parameters), balancing exploration versus exploitation becomes more intricate and traditional Bayesian methods do not scale well. Therefore, we introduce a new Dimension Scheduling Algorithm (DSA) to deal with high dimensional models. The DSA optimizes the fitness function only along a limited set of dimensions at each iteration. In each iteration, a random set of dimensions is selected to be optimized. This reduces the necessary computation time, and allows the dimension scheduling method to find good solutions faster than the traditional method. The increased computational speed stems from the reduced number of data points per each GP and the reduced input dimensions in the GP; GPs scale linearly in the number of dimensions but cubically in the number data points. Additionally, considering a limited number of dimensions at each node allows us to easily parallelise the algorithm.