Summary
We’re developing data-efficient strategies to reduce the number of experiments needed for chemical and pharmaceutical development and manufacturing.
What contributions have we made?
- Multi-objective optimization for tissue engineering (Mehrian et al., 2018, Olofsson et al., 2018). We extend Bayesian multi-objective optimization to the case of one analytical objective function and one black-box, i.e. simulation-based, objective function
- Design of experiments for model discrimination (Olofsson et al., 2019). We use Gaussian process surrogates in lieu of mechanistic models and thereby extend existing design and model discrimination methods to non-analytical models.
- Verify biomolecular networks (Sedgwick et al., 2021). We use Gaussian processes to model the discrepancy between experimental results and the designed response and a Bayesian optimization strategy to select the next sample points.
- Flow chemistry (Folch et al., 2022). We consider a setting where the expense of evaluating the function increases significantly with large input changes between iterations. We further assume we have to decide new queries before we finish evaluating previous experiments.
Software
ENTMOOT: Multi-objective black-box optimization using gradient-boosted trees
Alexander Thebelt developed ENTMOOT together with our BASF colleagues. ENMOOT manages multi-objective black-box optimization using gradient-boosted trees over mixed feature spaces and input constraints (Thebelt et al., 2021, Thebelt et al., 2022). Here is an introduction to ENTMOOT:
GPdoemd: Design of experiments for model discrimination
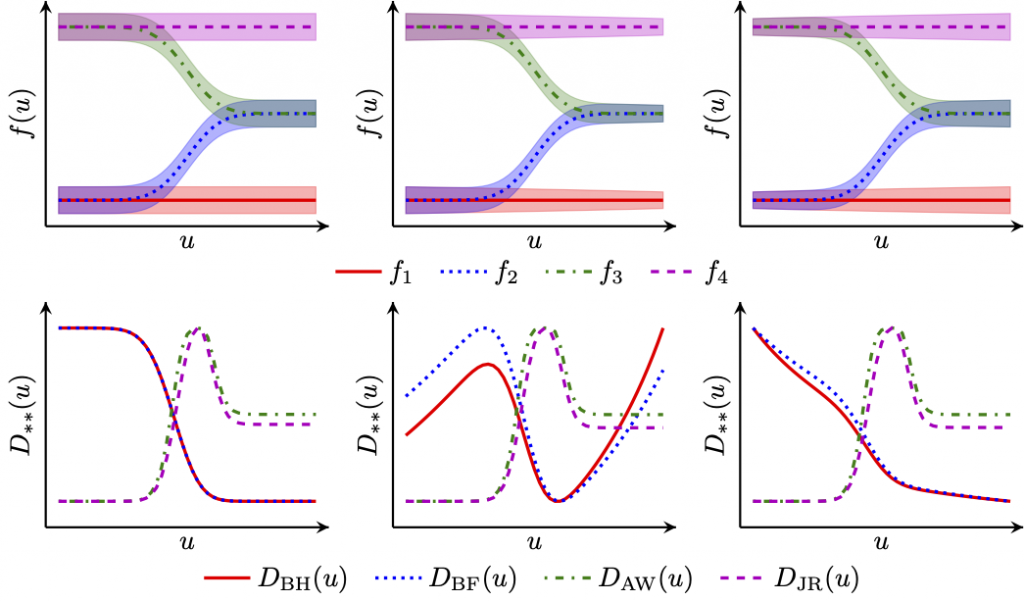
Dr Simon Olofsson’s GPdoemd uses Gaussian process surrogates to design the next experiment for model discrimination (Olofsson et al., 2018, Olofsson et al., 2019). Simon’s key question is: Where shall we take the next experiment? In the top row of the graph, there are several possible models f and we seek to discriminate amongst them for an input u. What should be the value of this input u? We select the value by optimizing one of several design functions D (bottom row).